前回のおさらい
これまで、統計学的手法による分析で積雪深の予測が可能かどうかを検討してきました。
統計的手法の代表例が線形回帰モデルであるため、これを用いて積雪深の予測をしたところ、決定係数が0.5、予測値と実測値の誤差が約18cmと大きな差があることが確認できました。
このことから、入力側の説明変数としていた「降水量」「気温」「湿度」「降雪量」と、出力側の目的変数である「積雪深」が実は線形な関係でないことが考えられたため、より複雑な関係性を捉えることができる非線形回帰モデルによる予測に切り替えました。
その結果、非線形回帰モデルでは決定係数がやや向上し、予測値と実測値との誤差も減少するなど、線形回帰モデルに比べて予測精度が比較的良好であることが確認されました。
ですが、まだまだ実用可能レベルとは言い難いです。
十分な精度を得られなかった原因として、収集したデータの量的な不足が主に考えられました。一般的にこのような数値を扱う分析は何十年分とデータを要するのに対して、前回収集した各気象データは約2年分であり学習には不十分である可能性があります。
この情報量の不足を画像処理で例えると、20x20pixの画像が1枚あるだけでも400pixの特徴量となります。仮に300枚集めたとすれば120,000pixの特徴量です。
このような情報量と比較すると、2年分の気象データは少なすぎることが明確ですね。
今回やること
少し脱線してしまいましたが、今回は各気象データと積雪深との複雑な非線形関係をより適切に捉えるため、機械学習手法の一つであるニューラルネットワークを用いた予測モデルの構築を試みます。
ニューラルネットワークを採用する理由の一つとして、ハイパーパラメータを調整することで予測精度の向上を期待しています。
加えて、学習に用いる気象データを約2年分から10年分に増量します。
ニューラルネットワーク
皆さん、ニューラルネットワークをご存知でしょうか。
現在、深層学習(ディープラーニング)はさまざまな分野で注目を集めており、その基盤となっているのがニューラルネットワークです。
深層学習の概念は理解しづらい面がありますが、現在最も応用されている分野として、自然言語処理、画像処理、音声処理などが挙げられます。
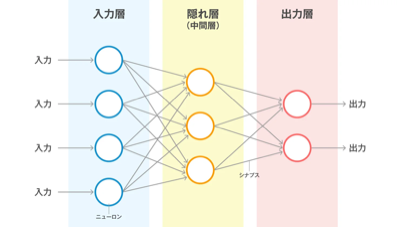
ニューラルネットワークは図のように入力層・中間層(隠れ層)・出力層から構成される階層的な構造を持っており、深層学習(ディープラーニング)は、中間層が複数連なった構造のニューラルネットワークを指しています。
従来の浅いニューラルネットワークでは中間層が1~2層であるのに対し、近年の深層学習モデルでは中間層が場合によっては4桁以上に及ぶこともあり、それによって画像や音声、言語といった高次元で非線形な特徴量を高精度で捉えることが可能となりました。

ニューラルネットワークの構造
機械学習
データ収集
前回までの統計学的手法である線形回帰モデルの分析では、説明変数が多すぎるとかえって目的変数である積雪深の予測精度が低下するという知見を得たため、7項目あった説明変数を「降水量」「気温」「湿度」「降雪量」の4項目に削減しました。
一方で、今回はニューラルネットワークを用いた機械学習手法を採用しており、高次元かつ多量のデータが学習精度の向上に寄与することが期待されます。
そこで、今回は気象庁が提供する気象データを最大限活用し、説明変数を「月」「日」「現地気圧」「海面気圧」「降水量」「気温」「湿度」「最大風速」「風向」「降雪量」「前日積雪深との差」の11項目に増やしました。
さらに、約10年分の長期間データに増量することで、モデルの学習に必要な情報量を大幅に増加させ、より精度の高い予測モデルの構築を目指します。
| month | day | land_atmosphere | sea_atmosphere | precipitation | temperature | humidity | wind_speed | wind_direction | snow_falling | melted_snow | snow_depth |
| 1 | 1 | 1017.8 | 1021.2 | 1 | -1.1 | 59 | 7.1 | 315 | 2 | 1 | 27 |
| 1 | 2 | 1008.9 | 1012.2 | 3.5 | 1.6 | 75 | 6.5 | 292.5 | 0 | 2 | 25 |
| 1 | 3 | 1009.9 | 1013.2 | 0 | 0.3 | 52 | 6.7 | 292.5 | 0 | 4 | 21 |
| 1 | 4 | 1009.1 | 1012.4 | 0 | -1.7 | 57 | 5.2 | 292.5 | 0 | 0 | 21 |
また説明変数の一つである風向は、元データでは「北北西」など16方位での表記となっていたため、これをニューラルネットワークで扱える数値に変換する方法を検討してみました。
下記のリンクを見てみると、北が0度で南が180度というように16方位それぞれに対応する角度に変換できることがわかりました。
この知見に基づき各方位に対応する角度に変換するソースコードを作成し実行したところ、上記の表のように風向情報を数値化することができました。
import pandas as pd
import csv, os, sys
csv = pd.read_csv(sys.argv[1])
# 風向きと角度の対応を辞書として定義
wind_direction_map = {
"北": 0,
"北北東": 22.5,
"北東": 45,
"東北東": 67.5,
"東": 90,
"東南東": 112.5,
"南東": 135,
"南南東": 157.5,
"南": 180,
"南南西": 202.5,
"南西": 225,
"西南西": 247.5,
"西": 270,
"西北西": 292.5,
"北西": 315,
"北北西": 337.5
}
# 風向き列を角度に変換
csv["wind_direction"] = csv["wind_direction"].map(wind_direction_map)
#角度なのでファイル名にangleを追加
output_filename = os.path.splitext(sys.argv[1])[0] + "_angle.csv"
# 変換後のデータをCSVファイルとして保存
csv.to_csv(output_filename, index=False)
学習
ニューラルネットワークの実装には、scikit-learnライブラリに含まれるMLPRegressorを使用しました。
# データの読み込み
file = pd.read_csv(sys.argv[1])
# display(df.head())
# df.shape
out_dir = pathlib.Path(sys.argv[2])
if(not out_dir.exists()): out_dir.mkdir()
# 入力変数と出力変数の設定
int_var = ["month", "day","land_atmosphere", "sea_atmosphere", "precipitation", "temperature", "humidity", "wind_speed", "wind_direction", "snow_falling", "melted_snow"] #入力
out_var = file["snow_depth"] #出力
# 入力/出力変数をデータフレーム化
x = file[int_var]
x.head()
y = out_var
y.head()
# データの分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
# データの標準化
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_test_scaled = scaler.transform(x_test)
# ニューラルネットワーク
pochSize = 500
model = MLPRegressor(hidden_layer_sizes=(128, 64, 32), activation="relu", solver="adam", alpha=0.002, learning_rate_init=0.001, random_state=60, early_stopping=True, max_iter=epochSize)
model.fit(x_train_scaled, y_train)
train_score = model.score(x_train_scaled, y_train)
test_score = model.score(x_test_scaled, y_test)
print(f"train_score : {train_score:.3f}")
print(f"test_score : {test_score:.3f}")冒頭でも記述したように、今回ニューラルネットワークを採用した理由の一つにはハイパーパラメーターの調整によりモデル精度の向上が期待できるからです。
ニューラルネットワークは、層の数や各層のニューロン数(ノード数)、学習率、活性化関数など多くのハイパーパラメーターを持っており、これらを適切に設定することで、予測性能の改善が可能となります。
まず調整したパラメーターは、中間層の構造を定義するhidden_layer_sizesです。今回はそれぞれ128, 64, 32個のニューロンからなる3層を設定しました。
中間層の数や各層のニューロン数は、学習データの性質や目的に応じて最適な構成が異なるため、複数のパターンを試行しながら調整することが望ましいと思います。
次に調整した活性化関数は、各ニューロンの出力を非線形に変換するものであり、深層学習においては学習能力や収束性に大きな影響を与える重要な要素です。活性化関数には一般的に使用される ReLUを選択しました。ReLUは学習が停滞しにくく、出力の安定性も高いという利点があります。
また、最適化関数(solver)にはadamを選択しています。これも深層学習において広く用いられる手法です。

評価
11項目の説明変数を入力として、積雪深を目的変数とした問題をニューラルネットワークで学習・予測させた結果、以下のような精度を得ることができました。

学習結果の比較をしたところ、訓練データに対する決定係数が0.8を超えておりモデルが十分にデータを学習できたことが確認できました。
さらに、訓練データとテストデータにおける決定係数の差は約0.08と小さく、過学習の兆候も見られませんでした。なお、この結果を見ながら中間層を増減させます。
また、予測値と実測値の誤差に関しても、前回の非線形回帰モデルと比較して誤差が7cmほど改善されており、ニューラルネットワークの導入による精度向上が確認できました。
以上の結果から、前回の非線形回帰モデルと比較して、ニューラルネットワークの方が本課題においてはより適した手法である可能性が考えられます。
おわりに
いかがでしたでしょうか。
今週はニューラルネットワークによる積雪深の予測をしてみました。
その結果、前回の非線形回帰モデルよりも精度/誤差ともに大きく向上していることが確認できました。
今回作成したソースコードは僕のgithubから使用いただけます。
必要なライブラリについてはreadmeに記載の方法でインストールできます!
参考URL